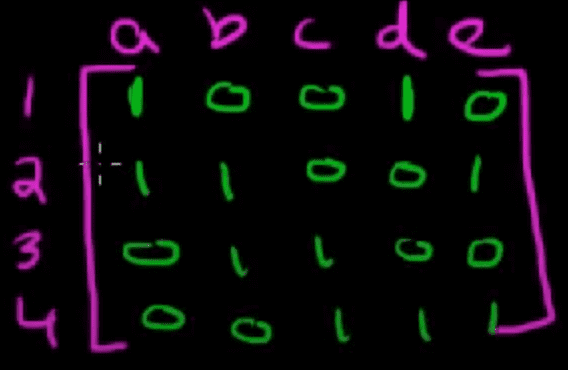In the last couple of weeks, I’ve been learning more about Graph Theory and today I learned why and how to represent a graph using matrices (matrices are a fancy computer-science term for multi-dimensional array which is another fancy computer-science term, ha!).

Before explaining the different ways to represent your graph, let’s define some terminology:

• Vertices: the nodes in the graph
• Degree of a vertex: the number of edges coming out of a vertex
• Edges: The lines connecting two vertices

There are two main ways that you can use to do that:

1) Adjacency Matrix (most common)

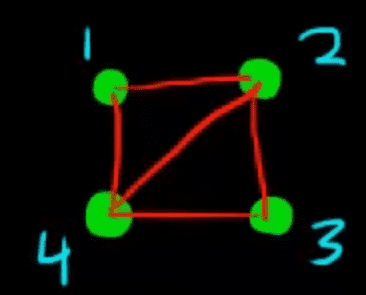
Let’s take this graph as an example

You can represent the same graph in this matrix:

Which is identical to what we can write in code as:

[
	[0,1,0,1],
	[1,0,1,1],
	[0,1,0,1],
	[1,1,1,0]
]

How to do that?

• Rows and columns both represent vertices
• Place 0 if there is no edge between those two vertices
• Place 1 if there is an edge between the two vertices
• Why cell 1~1 has a value of 0? because there is no edge between 1 and 1, it’s not a loop
• The row/column sum equals the degree of a vertex that the row represents. For example row 2 has 3 ones so its degree is 3 and in reality vertex 2 indeed has 3 edges

2) Incidence Matrix

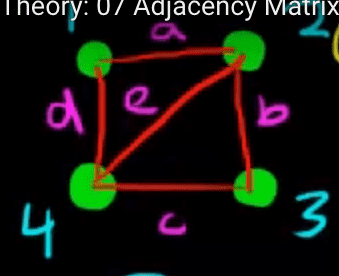
Let’s use this graph as an example:

You can represent the same graph in this matrix:

How is this matrix structured?

• Rows represent vertices
• Columns represent edges
• The value in the cell is 1 if the vertex belongs to the edge
• The value in the cell is 0 if the vertex is not on the edge
• The row sum represents the degree of the vertex. For example vertex 2 has 3 edges connected to it so it’s degree is 3
• The column sum will always equal 2 because any edge in any graph has two ends connecting it to two vertices. That’s basically just the definition of an edge that it has two edges in any given graph.

Why do we need that matrix representation?

It represent everything in the graph in a code-friendly way